來(lái)源:高(gāo)德技(jì)術(shù)
道(dào)路匹配是地圖數(shù)據處理(lǐ)方面非常基礎且重要的理(lǐ)論,特别是道(dào)路相關業務,一定避不開(kāi)道(dào)路匹配的應用,這也是業務中普遍會(huì)碰到的痛點。
道(dào)路匹配定義
道(dào)路匹配是地圖匹配理(lǐ)論的子集,通(tōng)俗講就是兩幅地圖A和(hé)B,在沒有(yǒu)唯一ID關聯的情況下,如何确定地圖A上(shàng)的道(dào)路是B上(shàng)一條道(dào)路的過程。如果做(zuò)交通(tōng)軌迹或者地圖數(shù)據融合方面的研究,那(nà)麽就一定會(huì)遇到地圖匹配的問題。
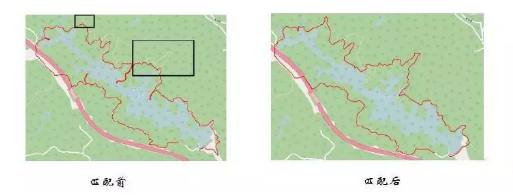
地圖匹配 Map Matching:不同條件下獲取同一物景的地圖之間(jiān)的配準關系。
道(dào)路匹配是刨除了點和(hé)面狀匹配之外的線狀要素理(lǐ)論,道(dào)路的話(huà)就是路網,也是實際應用中研究最多(duō)、應用最廣的一部分。
利用路網數(shù)據,采用适當算(suàn)法,将目标定位映射到實際道(dào)路上(shàng)的過程,具體(tǐ)來(lái)說道(dào)路匹配是:
l 地圖匹配理(lǐ)論的首要子集
l 針對矢量拓撲道(dào)路數(shù)據的匹配模式
l 異源道(dào)路數(shù)據融合的關鍵
l 導航定位精度改善的重要手段
空(kōng)間(jiān)距離和(hé)評價曲線相似性的一般方法
離散點集匹配
路網匹配的兩個(gè)方面應用:第一個(gè)是離散點集匹配,相對簡單,随機離散點沒有(yǒu)形狀和(hé)拓撲關系,用歐氏距離作(zuò)吸附即可(kě),典型應用如離散熱力圖。
曲線拟合
實際中更有(yǒu)應用價值的是曲線拟合匹配關系,比如軌迹和(hé)路網,GPS序列和(hé)導航路的相似性。
曲線信息更多(duō),這方面比離散點集有(yǒu)更多(duō)的評價要素,也有(yǒu)更高(gāo)的複雜度。評價曲線相似性的一般要素有(yǒu)長度、形狀、曲率、拓撲關系、方向比如正向逆向、距離、屬性例如交通(tōng)規則左轉右轉禁行(xíng)等信息。

曲線匹配方法分類
基于幾何信息的匹配算(suàn)法考慮形狀、角度等常規要素,屬于早期的一些(xiē)算(suàn)法,實現最簡單,準确度最低(dī)。基于拓撲信息的算(suàn)法,準确度比幾何方法大(dà)大(dà)提升,應用最廣。基于概率預測的算(suàn)法,實現比較困難,實際上(shàng)應用不多(duō)。
目前有(yǒu)一些(xiē)比較高(gāo)級的算(suàn)法理(lǐ)論,包括隐馬模型等等,在實際應用中準确度是相對最高(gāo)的。
實時(shí)算(suàn)法主要用于在線導航,時(shí)間(jiān)和(hé)空(kōng)間(jiān)複雜度低(dī),離線算(suàn)法用于數(shù)據處理(lǐ)的離線計(jì)算(suàn),算(suàn)法複雜,追求最高(gāo)準确度。
空(kōng)間(jiān)距離
線要素的匹配,主要通(tōng)過幾何、拓撲或語義相似度來(lái)進行(xíng)識别,其中通(tōng)過空(kōng)間(jiān)距離來(lái)進行(xíng)要素匹配的常用方式有(yǒu):
l 闵可(kě)夫斯基距離(Minkowski Distance)
l 歐氏距離(Euclidean Distance)
l 曼哈頓距離(Manhattan Distance)
l 切比雪夫距離(Chebyshev Distance)
l 漢明(míng)距離(Hamming distance)
l 傑卡德相似系數(shù)(Jaccard similarity coefficient)
l 豪斯多(duō)夫距離(Hausdorff Distance)
l 弗雷歇距離(Fréchet距離)
最準确的匹配模型-隐式馬爾科夫模型HMM
20世紀60年代,Leonard E. Baum和(hé)其它作(zuò)者在一系列的統計(jì)學論文中描述了隐式馬爾科夫模型。它最初的應用之一是語音(yīn)識别,80年代成為(wèi)信号處理(lǐ)的研究重點,現已成功用于故障診斷、行(xíng)為(wèi)識别、文字識别、自然語言處理(lǐ)以及生(shēng)物信息等領域。
核心特征
l 隐式馬爾科夫模型五要素:2個(gè)狀态集合和(hé)3個(gè)概率矩陣,Viterbi算(suàn)法。
l 隐含狀态S:馬爾科夫模型中實際所隐含的狀态,通(tōng)常無法通(tōng)過直接觀測得(de)到,這些(xiē)狀态之間(jiān)滿足馬爾科夫性質。
l 可(kě)觀測狀态O:通(tōng)過直接觀測而得(de)到的狀态,在隐式馬爾科夫模型中與隐含狀态相關聯。
l 狀态轉移概率矩陣A:描述隐式馬爾科夫模型中各個(gè)狀态之間(jiān)的轉移概率。
l 觀測狀态概率矩陣B:表示在t時(shí)刻隐含狀态是Sj條件下,其可(kě)觀測狀态為(wèi)Ok的概率。
l 初始狀态概率矩陣π:表示隐含狀态在初始時(shí)刻t=1的概率矩陣

路網匹配實際是一個(gè)解碼問題,基于HMM的路網匹配算(suàn)法是在一系列觀察的前提下,尋找最有(yǒu)可(kě)能産生(shēng)這個(gè)觀察序列的隐含狀态序列。一系列GPS位置點集合是可(kě)觀測狀态,尋找最有(yǒu)可(kě)能産生(shēng)位置點集合的路網隐藏序列。
2012年ACM SIGSPATIAL Cup是由ACM主辦的全球範圍內(nèi)關于地圖匹配算(suàn)法的科技(jì)競賽,競賽吸引了來(lái)自全球31支專業級的參賽隊伍。所有(yǒu)算(suàn)法當中匹配準确率最高(gāo)的兩個(gè)都是基于HMM的匹配算(suàn)法。